Introduction
After the previous post analyzing traditional guitar circuits, I have done more research on something that would be better. I have come up with two exciting circuits. Well I guess they're only exciting if you get excited about such things. Both allow direct maniupulation of the cutoff frequency of the circuit without a change in gain, and both are active.
1 Pole Circuit
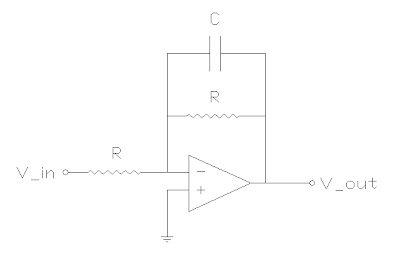
The first circuit is a standard 1 pole active filter. It uses an opamp, a capacitor, and two equal resistors for unity gain. Actually, the gain is -1 (not dB mind you), so it's an inverting amplifier. But we don't care too much about that.
The circuit is a variation on a standard opamp inverter, except now there is a capacitor in parallel with the feedback resistor. So higher frequencies get a lower feedback resistance, which decreases their gain. The equation for the magnitude of the gain in this circuit is as follows.
The cutoff frequency is the same as the passive 1 pole low pass filter.
So we can manipulate the cutoff frequency directly by adjusting R and keeping C constant. The values I chose were
Rtone = 100 Ohms
TonePot = 50KOhms
C = 0.22uF
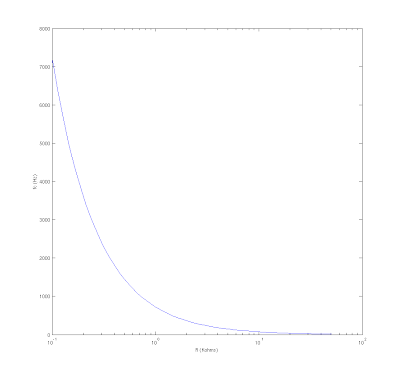
Rtone is put in series with both pots. So R = Rtone + Rtonepot. This gives us a stop at the high end of fc as seen on the graph. The range is 7.2Khz to 14 Hz. 7.2 Khz is very high to listen to alone. I will have to decide whether I like it as a maximum for the circuit. The idea is to crank the tone circuit all the way up and hardly affect the tone at all. So everything under 7.2Khz will be left untouched, and the response will start to drop off after that. But in all seriousness, the pickup itself probably will attenuate those frequencies quite a bit anyway.
**********
Note: This plot is not the correct graph. See Part 3 for a useful graph.
**********
There are two drawbacks to this circuit. Firstly, the frequency change is not linear with change in R. In fact, you'll notice that it is not even linear with changes in log(R). But it doesn't look too terrible with a log tone pot. And hey, we're going from no control to some control, so how upset can we be about nonlinearities. Secondly, it requires a dual-ganged pot. Both resistors much change by the same amount, or the overall magnitude of the gain will change as well. Basically, the inverting amplifier will begin to amplify or attenuate the signal. We only want that to happen when we adjust the volume pot. So there's no way around the problem.
2 Pole Circuit
The second circuit is a Butterworth filter implementation in a Sallen-Key topology. Here is the schematic.
I was pretty happy about the math on this one, so I'll give a little bit more detail. The general gain for the Sallen-Key topology is...
Where Z1 = R1, Z2 = R2, Z3 = 1/(C2s), Z4 = 1/(C1s)
The cutoff frequency and Q factor are given as follows.
We set Q = 1/sqrt(2) to achieve a Butterworth filter. This filter has a maximally flat frequency response prior to the cutoff frequency. Because this is a 2 pole filter, it drops off more steeply than the 1 pole filter described before. With the added steepness, which is desireable in many applications, comes the chance for a non-flat response in the "passband" (prior to the cutoff frequency). The filters tend to have a high peak near the cutoff frequency before dropping off. Designing Q = 1/sqrt(2) makes this peak disappear.
Lets set the resistances equal to each other so that we can use a dual-ganged pot and see what falls out of the equations.
When we plug this back into the Q equation, look what falls out...
That's great! We can totally eliminate the resonate peak around the cutoff frequency by making one capacitor double the other. And this holds true for all values of R, so the filter's response will not change as we adjust the cutoff frequcy. Now, how will that frequency be affected by changing the resistors now that we've come up with the above equations? Substituting in to the fc equation, we get...
That's the exciting part. I hope you're as excited as I am. The equation is almost exactly like the one we had for the 1 pole filter! The factor of sqrt(2) will tend to make our cutoff frequencies a little smaller, but it's a constant factor. Everything remains controllable from a single dual-ganged pot.
Choosing
Rtone = 1 KOhms
Rtonepot = 50 KOhms
C1 = 0.02uF
C2 = 0.01uF
We get the following plot for cutoff frequency.
As you can see, our cutoff frequency on the low end of the R range is higher, and we probably don't go quite as low when we max it out. Actually, for these values the lowest frequency is 220Hz, which is a little high. But different values will yield a better range.
Conclusion
I have shown two circuits with fully adjustable cutoff frequencies. The only drawbacks are the need for a power supply and the dual-ganged pot that will have to be added. For my own purposes, I am back to trying to make a 3-ganged pot. I should be able to do it, since my friend James offered to machine me some parts if I needed them. He's a nice guy.
I will be using the first circuit (1 pole), because it will be more like the original response of the original tone circuit. I realize that I no longer have the ability to flatten out the gain curve, but was that really even that useful? Now I can just move the cutoff frequency down the line and I won't attenuate anything anyway. In my opinion, these are vastly superior circuits. Still, I choose the 1 pole model, because I worry that the 2 pole would drop off too quickly. Plus the 1 pole is slightly easier to source parts for, due to the need for only 1 capacitor. (Yes you can just put two in parallel to get twice the capacitance).
The circuit is finally coming together. I will post the final schematic whenever I get a chance.
Thanks for reading,
Bill
Tuesday, June 8, 2010
Thursday, June 3, 2010
Guitar Tone Circuit Analysis
Introduction
In keeping with my guitar circuit project, I wanted to delve into what the tone circuit actually does. The results were very surprising to me. I discovered several things about the tone circuit and its implications to the design of my new active circuit.
Voltage Divider and Resistor/Impedance Combination
Let me make sure we're all on the same page with voltage dividers. This is a very basic idea for anyone familiar with electronics, but for those who aren't, it isn't very complicated. Recall the idea of voltage drop, that voltage across a resistor is distributed along its length evenly. If you tap the resistor at a specific point (which is what a pot does), then you will get the voltage at that point. What you're actually doing is dividing the resistor into two resistors in series, which is also known as a voltage divider.

This is your standard voltage divider.
 The two resistors can be two halves of a pot, two separate resistors, or theoretical equivalents to several resistors combined according to the following techniques.
The two resistors can be two halves of a pot, two separate resistors, or theoretical equivalents to several resistors combined according to the following techniques.
Series Resistors
Parallel Resistors
Quick definitions:
Series resistors are connected such that one lead on R1 is connected to one lead on R2 with no other components in between. (such as those in the voltage divider above)
Parallel resistors are connected such that each lead of R1 is connected to exactly 1 lead of R2 with no other components in between. (Take out the voltage source in the voltage divider, and the resistors are in parallel.
Finally, recall that impedance is resistance generalized over all frequencies. Capacitors and inductors have frequency dependant impedance. Resistors have frequency independant impedance with is equal to their resistance (ideally). Impedances combine exactly like resistances (series and parallel, that is)
Tone Circuit
Here I will simplify the pickup model to just an ideal voltage source and a series resistance (R int). The tone circuit is next in line and is parallel to the volume circuit.
As you can see, only two terminals of the tone pot are connected to the circuit. The third does nothing. This makes the pot a simple variable resistor. I will show the effect of the resistor later.
I have said that the capacitor impedance varies with frequency. The capacitor in my guitar is a 0.22uF. This is the plot of the magnitude of its impedance vs frequency. Strictly speaking, impedance has an imaginary component, so I am always graphing magnitude. But I will just use the term impedance to mean "magnitude of impedance."
So to analyze this circuit intuitively, let's first consider just the tone circuit and the pickup model. Crank the tone pot all the way down, so now we have just Rint in series with Ctone. This is a basic low pass filter. Look at it as a voltage divider. At low frequencies, the capacitor has a higher impedance, but as you move up the frequency range, the capacitor is a smaller and smaller proportion of the total load. So the filter passes low frequencies and attenuates high frequencies.
The tone circuit requires pickup resistance
One thing that I didn't realize until doing this analysis is that the tone circuit depends heavily on the resistance of the pickup itself. The half power frequency or cutoff frequency of the RC filter is
If you replace the pickup with an opamp, as I have done in the Active Circuit described in a previous post, then R=0, and your filter won't work. The cutoff frequency will be infinity. Ideally, the whole tone circuit will have no effect on the signal at all!
The Response of the Circuit
I pulled out trusty old Matlab and made a simulation of this circuit. My measured values on my guitar were as follows.
Rint = 10.87 KOhms
Ctone = 0.22 uF
Rtone = 0 Ohms - 500 KOhms
Rvol = 0 Ohms - 500 KOhms
The x axis is frequency from 20Hz to 20KHz (the entire audible range). The y axis is gain. A gain of 0 indicates no effect on the circuit. A gain less than zero indicates some attenuation to the volume at that frequency. The different lines represent different settings on the tone pot (i.e. different values of Rtone).
Short Graph Discussion
For those familiar with the Bode plot of an RC Filter, the bottom line should look familiar. It rolls off at 20dB per decade from the cutoff frequency of about 66Hz. (Maybe this is why my tone sounds terrible when turned all the way down). As we increase the value of Rtone, the frequency response flattens out until there is no attenuation at all to speak of.
If we were to remove the capacitor all together, then the filter would be a simple voltage divider. So when the capacitor's impedance becomes negligable compared to the impedance of Rtone, then the gain flattens out to approximately what a voltage divider would be. As Rtone increases, the range of effectiveness of Ctone becomes smaller and smaller until it doesn't really affect the signal at all.
Log vs. Linear Tone Pot
The Meaty Part: Analyzing the Effect of Rtone
Here's where things get a little more difficult to explain intuitively. I worked and worked to get an analytical solution to this circuit. I probably should not admit that, because it's a very simple circuit. But part of my problem was that I was convinced that my answer was wrong when it was not. Let me explain. The equation for the gain of the circuit is
Obviously, this is a not very intuitive. But how about an equation for the cutoff frequency?
Ok, this is a little bit better, but still not great. I can see that the equation is very similar to the original, except that R is replaced by an uninviting square root. Wait! Notice that under the right circumstances, the quantity under the square root is actually negative. If you're reading this blog, then you probably know that negative square roots will not produce real numbers.
This was the point at which I kept checking and rechecking my work. But then I realized, that this is exactly what we observe in the response plot above. After a certain setting on the tone pot, the response never dips below -3 dB. Just what is this setting? If we set the quantity under the square root greater than 0, then we get...
Very interesting! So pretty much all frequency responses of note fall within the range of 0-26KOhms on Rtone. That's only the first 5.2% of the pot!
To verify this result, I altered the simulation to graph only from 0-30KOhms. Here is the graph.
Obviously, we've spanned all of the useful range of frequency responses in the first 5.2% of the pot. But what is the effect on the cutoff frequency?


In keeping with my guitar circuit project, I wanted to delve into what the tone circuit actually does. The results were very surprising to me. I discovered several things about the tone circuit and its implications to the design of my new active circuit.
Voltage Divider and Resistor/Impedance Combination
Let me make sure we're all on the same page with voltage dividers. This is a very basic idea for anyone familiar with electronics, but for those who aren't, it isn't very complicated. Recall the idea of voltage drop, that voltage across a resistor is distributed along its length evenly. If you tap the resistor at a specific point (which is what a pot does), then you will get the voltage at that point. What you're actually doing is dividing the resistor into two resistors in series, which is also known as a voltage divider.

This is your standard voltage divider.
 The two resistors can be two halves of a pot, two separate resistors, or theoretical equivalents to several resistors combined according to the following techniques.
The two resistors can be two halves of a pot, two separate resistors, or theoretical equivalents to several resistors combined according to the following techniques.Series Resistors
Parallel Resistors
OR
Series resistors are connected such that one lead on R1 is connected to one lead on R2 with no other components in between. (such as those in the voltage divider above)
Parallel resistors are connected such that each lead of R1 is connected to exactly 1 lead of R2 with no other components in between. (Take out the voltage source in the voltage divider, and the resistors are in parallel.
Finally, recall that impedance is resistance generalized over all frequencies. Capacitors and inductors have frequency dependant impedance. Resistors have frequency independant impedance with is equal to their resistance (ideally). Impedances combine exactly like resistances (series and parallel, that is)
Tone Circuit
Here I will simplify the pickup model to just an ideal voltage source and a series resistance (R int). The tone circuit is next in line and is parallel to the volume circuit.
As you can see, only two terminals of the tone pot are connected to the circuit. The third does nothing. This makes the pot a simple variable resistor. I will show the effect of the resistor later.
I have said that the capacitor impedance varies with frequency. The capacitor in my guitar is a 0.22uF. This is the plot of the magnitude of its impedance vs frequency. Strictly speaking, impedance has an imaginary component, so I am always graphing magnitude. But I will just use the term impedance to mean "magnitude of impedance."
So to analyze this circuit intuitively, let's first consider just the tone circuit and the pickup model. Crank the tone pot all the way down, so now we have just Rint in series with Ctone. This is a basic low pass filter. Look at it as a voltage divider. At low frequencies, the capacitor has a higher impedance, but as you move up the frequency range, the capacitor is a smaller and smaller proportion of the total load. So the filter passes low frequencies and attenuates high frequencies.
The tone circuit requires pickup resistance
One thing that I didn't realize until doing this analysis is that the tone circuit depends heavily on the resistance of the pickup itself. The half power frequency or cutoff frequency of the RC filter is
If you replace the pickup with an opamp, as I have done in the Active Circuit described in a previous post, then R=0, and your filter won't work. The cutoff frequency will be infinity. Ideally, the whole tone circuit will have no effect on the signal at all!
The Response of the Circuit
I pulled out trusty old Matlab and made a simulation of this circuit. My measured values on my guitar were as follows.
Rint = 10.87 KOhms
Ctone = 0.22 uF
Rtone = 0 Ohms - 500 KOhms
Rvol = 0 Ohms - 500 KOhms
The x axis is frequency from 20Hz to 20KHz (the entire audible range). The y axis is gain. A gain of 0 indicates no effect on the circuit. A gain less than zero indicates some attenuation to the volume at that frequency. The different lines represent different settings on the tone pot (i.e. different values of Rtone).
Short Graph Discussion
For those familiar with the Bode plot of an RC Filter, the bottom line should look familiar. It rolls off at 20dB per decade from the cutoff frequency of about 66Hz. (Maybe this is why my tone sounds terrible when turned all the way down). As we increase the value of Rtone, the frequency response flattens out until there is no attenuation at all to speak of.
If we were to remove the capacitor all together, then the filter would be a simple voltage divider. So when the capacitor's impedance becomes negligable compared to the impedance of Rtone, then the gain flattens out to approximately what a voltage divider would be. As Rtone increases, the range of effectiveness of Ctone becomes smaller and smaller until it doesn't really affect the signal at all.
Log vs. Linear Tone Pot
I've heard some debate about log vs linear pots on tone circuits. Let me show you the difference. The original plot above is for a log pot. The steps on Rtone are spaced logarithically from 0 to 500K. The next plot is for a linear spacing between 0 and 500K.
Notice that the available responses are all grouped towards the top. There are very few response curves that are not practically flat. There are 50 steps between 0 and 500K in the simulation. Notice the vast difference between 0 ohms and the first step (10K or 1/50th setting on the pot). You will be pretty much unable to get any responses between those two, unless you have very very steady hands.
So I believe this is pretty strong evidence that maximum control over the tone can be had using a logarithmic pot instead of a linear pot.
The Meaty Part: Analyzing the Effect of Rtone
Here's where things get a little more difficult to explain intuitively. I worked and worked to get an analytical solution to this circuit. I probably should not admit that, because it's a very simple circuit. But part of my problem was that I was convinced that my answer was wrong when it was not. Let me explain. The equation for the gain of the circuit is
Obviously, this is a not very intuitive. But how about an equation for the cutoff frequency?
Ok, this is a little bit better, but still not great. I can see that the equation is very similar to the original, except that R is replaced by an uninviting square root. Wait! Notice that under the right circumstances, the quantity under the square root is actually negative. If you're reading this blog, then you probably know that negative square roots will not produce real numbers.
This was the point at which I kept checking and rechecking my work. But then I realized, that this is exactly what we observe in the response plot above. After a certain setting on the tone pot, the response never dips below -3 dB. Just what is this setting? If we set the quantity under the square root greater than 0, then we get...
Very interesting! So pretty much all frequency responses of note fall within the range of 0-26KOhms on Rtone. That's only the first 5.2% of the pot!
To verify this result, I altered the simulation to graph only from 0-30KOhms. Here is the graph.
Obviously, we've spanned all of the useful range of frequency responses in the first 5.2% of the pot. But what is the effect on the cutoff frequency?

Answer: Pretty dismal. Yes there is a big peak at about 17KOhms, but if you look at the x axis, the majority occurrs between 15Kohms and 17Kohms. Other than that, the response is pretty flat. So we're taking about most of the change in frequency is between 3% and 3.4% of the pot. Not very practical.
By the way, the reason for the descrepancy between 17KOhms as the cutoff and 26KOhms is because I neglected Rvol in my analytical solution.
Apparently, adjusting Rtone is a crappy way to move the cutoff frequency.
Load Presented to the Pickup
I also checked the load impedance to the pickup. As I've shown in a previous post, the values of the pots greatly affect the signal strength and frequency output of the pickups. So it is of interest to us how adjusting the tone pot will affect the load on the pickups. Here is the chart.

If you do the math, the parallel combination of the two pots is 250K. Looking at the plot, the larger Rtone becomes, the more closely the load approaches 250K. The impedance of the capacitor was shown early in this post. So basically, low tone pot settings will cause a double whammy effect on cutting the highs. Since I didn't model the pickup with any inductance, this is not shown in the simulation, but you can combine the earlier article on pot resistances with this one to see that the effect will be heightened. Both the low impedance load and the low pass filter will tend to cut the highs out of the signal.
Conclusion
That was a lot of information about the tone circuit in a guitar. Here's the source code for my simulation...
% tone control simulation % 0.022 uF capacitor Ctone = 0.22e-6; % 500 Kohms Tone Pot Rtone = 500e3; % 500 Kohms Volume Pot Rvol = 500e3; % pickup resistance 10.87 Kohms Rpickup = 10.87e3; %actual guitar value %Rpickup = 10; %opamp output impedance worst case %Rpickup = 100e3; %for more cutoff frequency change % steps on the tone resistor %toneres = logspace(0, log10(Rtone)); %toneres = linspace(0, Rtone, 50); %toneres = logspace(1,log10(30e3)); toneres = linspace(0,30e3,50); % steps in frequency %freq = [ 20:10:20000]; freq = logspace(log10(20), log10(20e3), 100); ZCtone = repmat( (-j./(2*pi*Ctone.*freq)) , size(toneres,2),1); Ztone = repmat(toneres',1,size(ZCtone,2)) + ZCtone; Zeq = Ztone .* (Rvol*ones(size(Ztone))) ./ (Ztone + Rvol*ones(size(Ztone))); gain = abs(Zeq ./ ( Zeq + Rpickup*ones(size(Zeq))))'; fc = 1./(2*pi*Ctone*sqrt(Rpickup^2*ones(size(toneres)) + Rpickup*toneres - toneres.^2)); % look at the capacitor impedance figure(1); semilogx(freq,abs(ZCtone)/1000); xlabel('Frequency (Hz)'); ylabel('Magnitude of Capactior Impedance (KOhms)'); % total magnitude of load presented to pickup figure(2); semilogx(freq,abs(Zeq)/1000); xlabel('Frequency (Hz)'); ylabel('Magnitude of Load Impedance (kOhms)'); % plot gain of circuit figure(3); semilogx(freq,20*log10(gain)); xlabel('Frequency (Hz)'); ylabel('Gain (dB)'); % plot fc of circuit figure(4); plot(toneres/1000,real(fc)); xlabel('Rtone (KOhms)'); ylabel('Cutoff Frequency (Hz)'); I hope that this has been enlightening to you. It certainly was for me. Basically tone control circuits are pretty crappy. I have done some research into better circuits, especially active ones. You can directly adjust the cutoff frequency using Sallen-Key filters by adjusting the two resistors and keeping the capacitors constant. This is a good thing, since variable capacitors are not very practical for guitar circuits. I will post more on this topic when I have come to some more conclusions. As always, thanks for reading. Bill
Subscribe to:
Posts (Atom)